Saat kelas X dalam matematika dikenalkan adanya fungsi linear. Fungsi linear merupakan suatu fungsi yang pangkat tertinggi dari variabel bebasnya adalah 1 dengan m sebagai gradien atau slope garis dan n sebagai konstanta. Fungsi ini ditentukan dengan cara menentukan dua titik yang ada pada persamaan garis lurus tersebut.
Fungsi Linear
Pengertian fungsi adalah hubungan matematis antara variabel satu dengan variabel lainnya. Unsur pembentuk fungsi yakni terdapat variabel, konstanta, koefisien. Variabel memiliki makna yaitu sebuah unsur yang sifatnya berubah ubah dari kondisi satu ke kondisi lainnya. variabel dibedakan menjadi 2 yaitu:
Variabel bebas: variabel yang menjelaskan variabel lainnya.
Variabel terikat: variabel yang diterangkan oleh variabel bebas.
Kemudian dalam fungsi terdapat koefisien yaitu bilangan atau angka yang berada di depan suatu variabel dan terkait dengan variabel yang bersangkutan. Konstanta memiliki sifat yang tidak terkait dengan suatu variabel manapun. Fungsi linier dapat dirumuskan sebagai berikut:
Variabel, koefisien, konstanta
F(x)=mx+n
– F(x) menandakan adanya fungsi
– m menandakan sebuah koefisien yang menempel pada x, huruf m pada fungsi linear merupakan gradien atau kemiringan bisa disebut juga kecondongan.
– n menandakan adanya sebuah konstanta
fungsi linear adalah sebuah fungsi f(x) atau sama dengan y dengan syarat f(x)=ax+b untuk seluruh x dalam daerah asalnya. Fungsi ini juga disebut sebagai dungsi polinom atau suku banyak berderajat satu dalam variabel x.
untuk paham fungsi linear dalam matematika perlu tahu bagaimana cara untuk melukis grafik fungsi linier. Berikut adalah Langkah untuk melukis grafik:
- Menentukan titik potong dengan sumbu x,y=0 didapatkan koordinat A(x1,0)
- Menentukan titik potong dengan sumbu y,x=0 didapatkan koordinat B(0,y1)
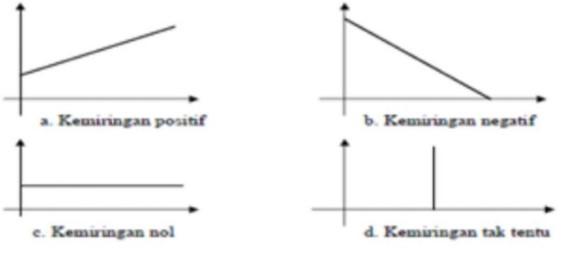
- Menghubungkan dua titik A dan B yang akan terbenuk garis lurus persamaan linier yang bisa juga ditulis dengan simbol y=ax+b. Dari fungsi tersebut maka diketahui jika b bernilai positif maka fungsi linear akan dilukis dengan gambar garis dari kiri bawah ke kanan atas. Jika b bernilai negative maka fungsi linier akan digambarkan garis dari kiri atas ke kanan bawah. Jika b bernilai nol maka fungsi linier akan digambarkan garis yang sejajar dengan sumbu datar x.
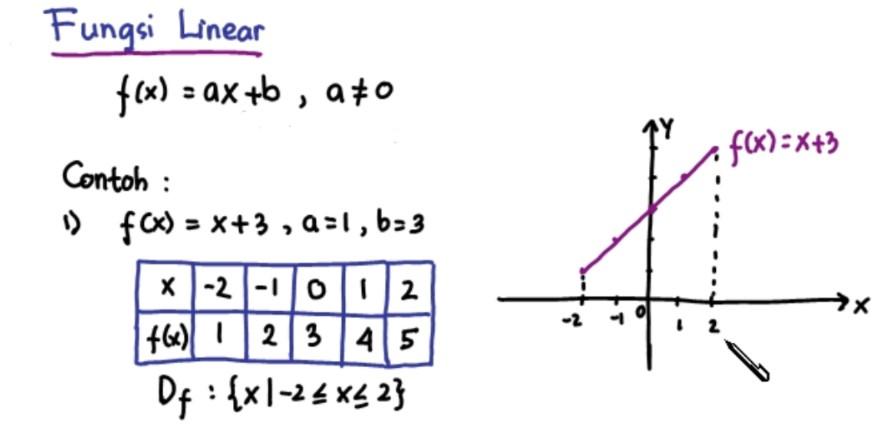
Gambar dibawah merupakan grafik fungsi linear
Contoh
Untuk penjelasan gambar diatas terdapat pembatasan domain fungsi x dari -2 sampai dengan 2. Fungsi yang didapatkan adalah hasil perkalian rumus fungsi dengan variabel x yang tersedia dari domain.
Gradien serta Persamaan Garis lurus Fungsi Linear
Pada fungsi linear terdapat gradien dan persamaan garis lurus dengan rumus sebagai berikut.
1. Apabila garis lurus yang melewati titik A(x1,y1) dan B(x2, y2) memiliki gradien m:
m = y1=y2 atau m = y2-y1
x1-x2 x2-x1
2. persamaan garis lurus jika melewati titik A(x1,y1) dan B(x2,y2)
y-y1 = x=x1
y2-y1 x2-x1
3. persamaan garis lurus (pgl) yang bergradien m serta melewati titik A(x1,y1)
y = m(x-x1) + y1
Menentukan gradien dari persamaan garis lurus (PGL)
Untuk menentukan gradien dari persamaan garis lurus (pgl) pada fungsi linear sebagai berikut
-persamaan garis lurus:ax+by=c dari sini gradien m = -a/b
-persamaan garis lurus:y=ax+b, m = a
-garis yang sejajar dengan sumbu x memiliki persamaan y = c dan juga m= 0
-garis yang sejajar dengan sumbu y mempunyai persamaan x=c serta tidak memiliki gradien.
Pada fungsi linear terdapat titik potong dua buah garis lurus identic dengan menyelesaikan permasalahan dari sistem persamaan linier dua variabel yang dilakukan dengan metode eliminasi, substitusi maupun grafik. Sedangkan pada fungsi linier hubungan dua buah garis yaitu dua garis yang bergradien m1 dan m2 akan disebut sejajar jika m1 = m2 dan tegak lurus jika m1 x m2= -1
Berikut ini adalah rumus dua garis jika berimpit
apabila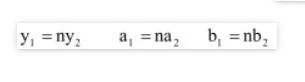 
Jika dua garis sejajar
Jika dua garis berpotongan, maka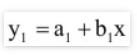 
Akan berpotongan dengan garis 
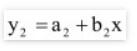apabila 
Tegak lurus
berpotongan
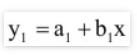akan berpotongan dengan garis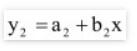 
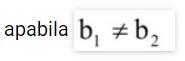
Persamaan kuadrat fungsi linear
Untuk persamaan kuadrat fungsi linear memiliki bentuk umum :
Dalam menentukan akar-akar persamaan kuadrat dapat dilakukan dengan beberapa metode:
Metode pemfaktoran:
Metode rumus abc
Contoh soal fungsi linear
- jika f(x) =4x-1 maka nilai f(-5) adalah
Pembahasan:
F(x) = 4x-1
F(-5) = 4.-5-5
F(-5) = -20 -5 = -25
Berikut adalah contoh soal mengenai fungsi linear dalam kehidupan sehari-hari.
Sebuah angkutan mobil menetapkan tarif awal sebesar Rp 20.000 dan untuk tarif selanjutnya akan dikenakan Rp 15.000 per km. Jika pak amar menyewa angkutan mobil dan menempuh perjalanan sejauh 20km. berapa biaya yang perlu dikeluarkan oleh pak amar untuk membayar angkutan umum?
Jawab:
Untuk menjawab soal diatas perlu untuk permisalan sebagai berikut:
Tarif angkutan= f(x)
Tarif per km= x
Maka:
F(x) = 15.000x + 20.000
F(20) = 15.000. 20 + 20.000
F(20) = 320.000
Jadi biaya yang perlu dikeluarkan pak amar untuk membayar angkutan mobil adalah Rp 320.000
Demikian penjelasan mengenai fungsi linear dan contohnya semoga anda dapat mengerti dan paham dengan materi matematika ini.
Baca Juga: 10 Rekomendasi Sewa Mobil Padang Terbaik
