Saat di sekolah kita pasti mengenal matematika. Iya matematika yang menurut banyak orang sebagai mata pelajaran tidak mengasikkan dan bikin pusing.
Namun bagi mimin matematika adalah mata pelajaran yang mengasikkan loh! Apalagi tentang rumus pitagoras segitiga. Wahh kesukaan mimin banget mata pelajaran itu.
Pitagoras Segitiga
Pitagoras segitiga merupakan bangun pada segitiga yang terdapat tiga sisi yang diantaranya adalah sisi tegak, sisi lurus, dan sisi miring. pitagoras memiliki sebuah rumus yang disebut dengan rumus pitagoras segitiga.
Untuk mengenal pitagoras segitiga dikenalkan sebuah teorema pitagoras adalah aturan matematika yang digunakan untuk menentukan panjang salah satu sisi dari suatu segitiga siku-siku. Teorema pitagoras membahas tentang segitiga siku-siku, sisi miring, dan sisi yang belum diketahui nilainya . Segitiga siku-siku memiliki sudut 90 derajat.
Rumus pitagoras segitiga dapat dibuktikan secara sistematis dalam ilmu matematika. Rumus ini menjadi salah satu metode untuk mengungkapkan sisi-sisi yang belum diketahui dalam segitiga.
Teorema pitagoras memiliki sifat-sifat sebagai berikut:
-hanya berlaku untuk segitiga siku-siku
-minimal terdapat dua sisi yang diketahui terlebih dulu.
Teorema pitagoras merupakan jalan mengungkap sisi dalam segitiga, namun untuk mengungkapkan dengan teorema pitagoras perlu mengenal karakteristik dalam suatu segitiga. Karakteristik suatu segitiga yaitu:
-jika kuadrat sisi miring sama dengan jumlah kuadrat sisi lain, maka segitiga tersebut adalah segitiga siku-siku
-jika kuadrat sisi miring < jumlah kuadrat sisi lain, maka segitiga tersebut adalah segitiga lancip
-jika kuadrat sisi miring > jumlah kuadrat sisi lain, maka segitiga tersebut adalah segitiga tumpul.
Teorema pitagoras merupakan pengungkap sisi segitiga siku-siku, oleh karena itu perlu melakukan identifikasi terhadap segitiga siku-siku. Berikut ini merupakan segitiga siku-siku.
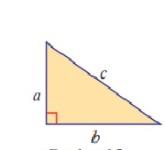
Bangun diatas merupakan segitiga siku siku yang memiliki tiga sisi panjang yang berbeda. a adalah bagian dari sisi segak segitiga. b merupakan sisi alas dalam segitiga siku-siku, dan c adalah sisi miring atau hipotenusa. Sisi miring berada tepat didepan siku-siku dalam sebuah segitiga.
Rumus pitagoras segitiga
Rumus pitagoras segitiga didapatkan dari materi teorema pitagoras. Teorema sendiri merupakan teori yang menjelaskan adanya hubungan antara sisi-sisi pada segitiga siku-siku. Rumus pitagoras dikenalkan oleh filsuf Yunani phytagoras. Rumus pitagoras digunakan untuk mencari panjang sisi miring segitiga siku-siku.
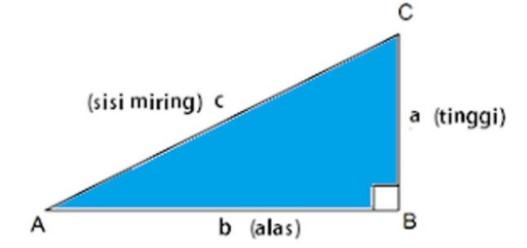
Berikut ini merupakan rumus pitagoras:
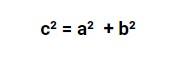
Keterangan:
c adalah sisi miring segitiga dalam rumus pitagoras
a adalah tinggi segitiga dalam rumus pitagoras
b adalah alas segitiga dalam rumus pitagoras
Berikut ini rumus untuk memudahkan anda mencari sisi segitiga menggunakan rumus pitagoras.
Untuk mencari panjang sisi alas segitiga menggunakan rumus pitagoras:
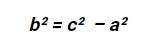
Untuk mencari panjang sisi samping atau tinggi segitiga menggunakan rumus pitagoras:
![]()
Untuk mencari sisi miring segitiga siku-siku menggunakan rumus pitagoras:
![]()
Dalil teorema pitagoras
Perlu diketahui pada rumus pitagoras terdapat dalil teorema pitagoras yang bermanfaat untuk menentukan panjang salah satu sisi segitiga yang tidak diketahui. Dalil tersebut berguna untuk perhitungan yang diantaranya adalah
-menentukan panjang diagonal dalam persegi
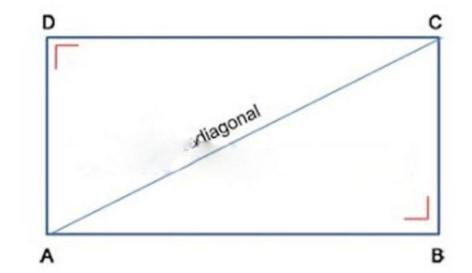
Menentukan panjang diagonal persegi digambarkan sebagai berikut.
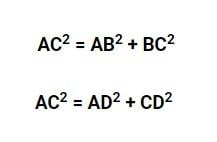
keterangan:
AC adalah garis yang disebut dengan diagonal persegi. jika panjang sisi persegi diketahui maka diagonal persegi diatas dapat dihitung menggunakan dalil pitagoras.
-menentukan diagonal ruang kubus dan balok
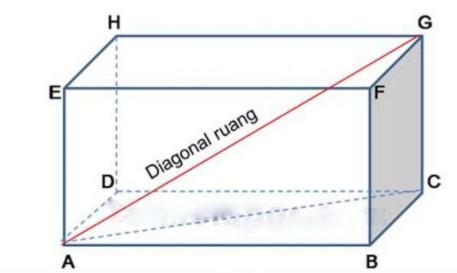
Pada gambar diatas garis AG adalah salah satu diagonal dari bangun ruang balok. Panjang diagonal tersebut dapat dihitung menggunakan dalil pitagoras.
rumus yang dapat digunakan untuk menghitung diagonal diatas adalah.
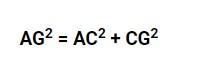
Keterangan:
AG adalah diagonal bangun ruang
AC adalah diagonal alas pada bangun ruang balok
CG adalah tinggi bangun ruang balok
Tripel pitagoras
Pada rumus pitagoras segitiga dikenalkan yaitu tripel pitagoras yang merupakan berbagai bilangan bulat positif yang kuadrat bilangan terbesarnya memiliki nilai yang sama dengan jumlah dari kuadrat bilangan-bilangan lain. Tripel pitagoras membentuk pola yang memiliki fungsi menyelesaikan soal pitagoras.
Macam-macam bilangan pitagoras contohnya sebagai berikut.
3 4 5 dan kelipatannya seperti 6 8 10; dst
5 12 13 dan kelipatannya, dst
7 24 25
8 15 17
9 12 15
10 24 26
12 16 20
12 35 37
13 84 85
14 48 50
dst
Contoh Soal dan pembahasannya
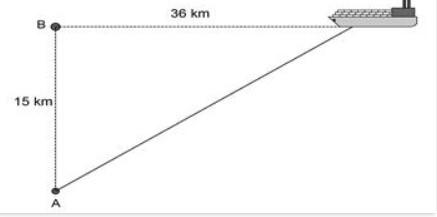
1. sebuah perahu diketahui berlayar dari pelabuhan A ke pelabuhan B sejauh 15km menuju utara. sesudah di pelabuhan B. Kemudian kapal tersebut berlayar lagi sejauh 36 km menuju arah timur. tentukan jarak antara pelabuhan A dengan titik akhir!
Pembahasan:
Dari gambar diatas dapat kita peroleh informasi bahwa
a adalah 15 km dan b adalah 36 km
jarak pelabuhan A ke titik akihr yaitu:
![]()
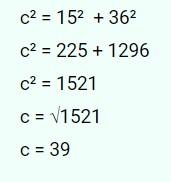
maka jarak pelabuhan A ke titik akhir sejauh 39 km
2. Diketahui bahwa ada segitiga siku siku memiliki ukuran dua sisi yang berpenyiku adalah 21 cm dan 28 cm. tentukan panjang sisi yang lain.
Pembahasan:
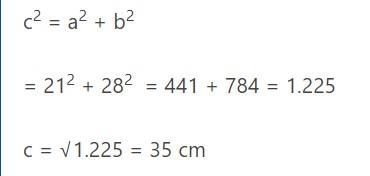
Demikian penjelasan tentang rumus segitiga pitagoras semoga dapat menambah wawasan anda. Good luck!
Baca Juga: Contoh Kalimat Majemuk Setara Terlengkap
