Tentunya, kita semua mengenal bilangan Fibonacci (atau disebut juga barisan Fibonacci). Suku pertama barisan ini adalah 1, begitu pula dengan suku ke-2. Suku berikutnya merupakan penjumlahan 2 suku sebelumnya.
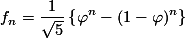
dimana
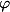 =
= 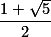
=========================================================================
Sepasang kelinci muda (jantan dan betina) ditempatkan di suatu pulau. Asumsikan bahwa kelinci tidak akan melahirkan sebelum berumur 2 bulan. Kemudian, setelah berumur 2 bulan, setiap pasang kelinci akan melahirkan sepasang kelinci setiap 1 bulan. Pertanyaannya: Berapa banyak pasang kelinci yang ada di sana setelah n bulan? (Kita juga menggunakan asumsi bahwa kelinci tidak akan pernah mati.)
Kita dapat mengilustrasikan masalah kelinci itu seperti tabel di bawah.
Asumsikan bahwa gambar 1 kelinci berarti 1 pasang kelinci.
| Keterangan: | |
 |
= kelinci muda |
 |
= kelinci 1 bulan |
 |
= kelinci berumur ≥ 2 bulan |
| Bulan ke- | Ilustrasi kelinci yang ada di pulau | Total pasang kelinci |
| 1 |  __ 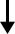 |
1 |
| 2 |  __ 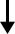 |
1 |
| 3 | ___ 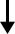 ______ ______ |
2 |
| 4 | ___ 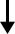 ______ ______  __ __ |
3 |
| 5 | ___  ______ ______  __ __ ____ ____  |
5 |
| 6 | 8 | |
| 7 | dan seterusnya… | 13 |
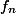 .
.
Barisan Fibonacci dapat didefinisikan kembali sebagai berikut:
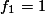
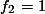 .
.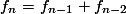 untuk
untuk 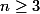
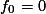 .
.
Untuk selanjutnya, barisan Fibonacci ini muncul dalam berbagai macam aplikasi. Sebagai contoh, di dalam bidang pertanian, jumlah pola spiral yang muncul pada tanaman (sering disebut sebagai phyllotaxis) selalu merupakan pola barisan Fibonacci.
=========================================================================
Dalam hubungannya mencari jumlah n suku pertama, pembicaraan kita tak terlepas dari deret. Kita beri simbol 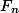 untuk menyatakan jumlah n suku pertama tersebut
untuk menyatakan jumlah n suku pertama tersebut
Note: Pemberian simbol 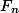 untuk deret Fibonacci ini tidak universal, dan tidak berlaku di tempat lain.
untuk deret Fibonacci ini tidak universal, dan tidak berlaku di tempat lain.
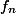 dan
dan 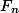 .
.Tabel
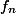 (barisan Fibonacci)
(barisan Fibonacci)
| f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Tabel 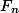 (deret Fibonacci)
(deret Fibonacci)
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| 1 | 2 | 4 | 7 | 12 | 20 | 33 | 54 | 88 | 144 |
Jelas bahwa kita menemukan identitas berikut:
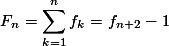
berlaku untuk
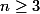 .
.Kita tahu bahwa
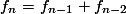 untuk
untuk 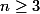 . Jika kita mensubstitusikan
. Jika kita mensubstitusikan 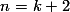 , maka pernyataan sebelumnya bermakna sama dengan:
, maka pernyataan sebelumnya bermakna sama dengan: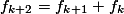 untuk
untuk 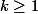 . Atau, jika kita tulis ulang dengan pemindahan ruas, akan sama dengan:
. Atau, jika kita tulis ulang dengan pemindahan ruas, akan sama dengan:
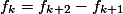 untuk
untuk 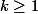
Oleh karena itu:
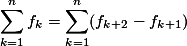
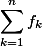 =
= 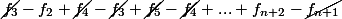
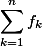 =
=
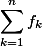 =
=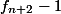
=========================================================================
== RUMUS BINET==
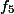 ) dari barisan fibonacci, tentunya kita lakukan dengan cara menghitung ulang secara 5 kali. Lebih tepatnya, kita melakukan penjumlahan 5 kali. Lalu bagaimana dengan
) dari barisan fibonacci, tentunya kita lakukan dengan cara menghitung ulang secara 5 kali. Lebih tepatnya, kita melakukan penjumlahan 5 kali. Lalu bagaimana dengan 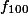 atau
atau 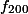 ? Mampukah kita menghitungnya? Jawabanya: tentu saja sanggup, tapi memakan waktu lama. Cara yang lebih baik yaitu dengan menggunakan komputer, karena komputer mampu menghitung dengan sekejab. Namun, tetap saja, algorima yang digunakan haruslah rekursif, yaitu seperti definisi fungsi Fibonacci sebelumnya di atas. Apakah ada formula lain yang mampu menghitung secara jauh lebih cepat, tanpa melakukan perhitungan secara rekursi?? Jawabnya adalah YA.
? Mampukah kita menghitungnya? Jawabanya: tentu saja sanggup, tapi memakan waktu lama. Cara yang lebih baik yaitu dengan menggunakan komputer, karena komputer mampu menghitung dengan sekejab. Namun, tetap saja, algorima yang digunakan haruslah rekursif, yaitu seperti definisi fungsi Fibonacci sebelumnya di atas. Apakah ada formula lain yang mampu menghitung secara jauh lebih cepat, tanpa melakukan perhitungan secara rekursi?? Jawabnya adalah YA.
Berikut diberikan formula (rumus Binet) untuk menentukan suku ke-n dari barisan fibonacci.
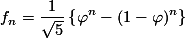
dimana
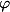 =
= 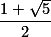 .
.
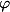 ) sering disebut juga sebagai golden number. Nilai
) sering disebut juga sebagai golden number. Nilai 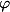 juga sama dengan
juga sama dengan  atau mendekati
atau mendekati 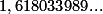
Sebagai contoh n = 9. Maka:
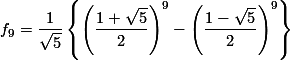
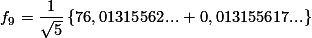
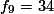
Hasilnya tidak diragukan lagi. Memang sama..!!
Barisan Fibonacci merupakan barisan kombinasi linear 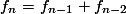 . Namun, kita juga dapat mendekati barisan ini secara geometrik.
. Namun, kita juga dapat mendekati barisan ini secara geometrik.
Asumsikan bahwa: 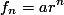 dimana a merupakan konstanta awal yang bukan nol. Dengan demikian:
dimana a merupakan konstanta awal yang bukan nol. Dengan demikian:
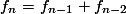
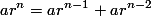
Dengan membagi kedua ruas dengan 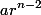 , kita dapatkan:
, kita dapatkan:
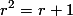
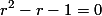
Bentuk di atas merupakan bentuk persamaan kuadrat. Oleh karena itu, kita gunakan rumus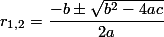 untuk menyelesaikan persamaan tersebut. Maka, kita dapatkan:
untuk menyelesaikan persamaan tersebut. Maka, kita dapatkan: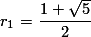 dan
dan 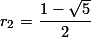 . Untuk mempermudah penulisan, kita tahu bahwa hasil dari
. Untuk mempermudah penulisan, kita tahu bahwa hasil dari 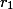 merupakan golden number, maka kita simbolkan dengan
merupakan golden number, maka kita simbolkan dengan 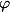 . Hasil dari
. Hasil dari 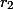 juga ternyata adalah
juga ternyata adalah 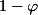 .
.
Kita mendapatkan 2 buah r dalam barisan ini. Artinya, barisan fibonacci merupakan barisan geometri kombinasi menggunakan 2 buah rasio tersebut. Ingat kembali asumsi awal bahwa 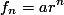 . Karena, kita memiliki 2 buah rasio r, maka kita definisikan kembali
. Karena, kita memiliki 2 buah rasio r, maka kita definisikan kembali
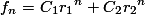
dimana
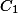 dan
dan 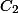 adalah konstanta bukan nol.
adalah konstanta bukan nol.Kombinasi linear tersebut dapat dibuktikan kebenarannya, seperti yang ditunjukkan di kotak warna biru di bawah.
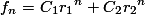 .
.Kita buktikan secara induksi matematika. Anggap bahwa 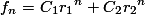 adalah BENAR.
adalah BENAR.
Kita tahu bahwa: 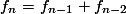 , maka:
, maka:
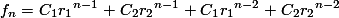
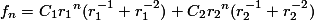
Namun, kita tahu dari persamaan karakteristik sebelumnya bahwa 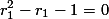 dengan membaginya dengan
dengan membaginya dengan 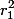 , kita dapatkan
, kita dapatkan 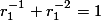 . Begitu pula dengan
. Begitu pula dengan 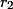 , kita dapatkan
, kita dapatkan 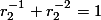 .
.
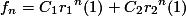
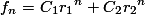
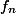 sesuai dengan definisi awal, maka
sesuai dengan definisi awal, maka 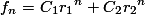 TERBUKTI secara induksi matematik.
TERBUKTI secara induksi matematik.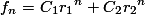
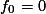
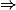
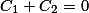 … (a)
… (a)
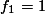
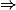
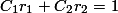
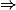
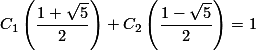 … (b)
… (b)
Dengan menyelesaikan persamaan (a) dan (b), maka kita dapatkan 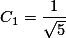 dan
dan 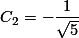 .
.
Maka, kita sudah mendapatkan semua komponen formula Fibonacci.
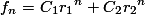
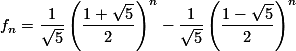
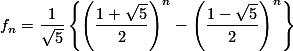
Dapat disingkat menjadi:
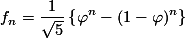
dimana
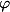 =
= 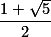 .
.
=========================================================================
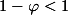 , maka
, maka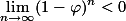 . Jadi, kita bisa meniadakan unsur
. Jadi, kita bisa meniadakan unsur 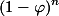 . Maka, hampiran rumus Binet adalah sebagai berikut.
. Maka, hampiran rumus Binet adalah sebagai berikut.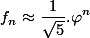
untuk n cukup besar.
Sebenarnya, masih banyak lagi identitas Fibonacci yang ada. Salah satunya sudah dibahas di atas, yaitu 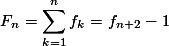 . Namun, karena identitas-identitas tersebut sangat banyak dan saya sedikit malas untuk membuatnya, dan juga karena keterbatasan tempat di post ini, maka sebaiknya materi tersebut dibahas lain waktu. Kalau ada request untuk membuat materi mengenai identitas-isentitas Fibonacci, maka saya akan segera membuatnya.. ^^
. Namun, karena identitas-identitas tersebut sangat banyak dan saya sedikit malas untuk membuatnya, dan juga karena keterbatasan tempat di post ini, maka sebaiknya materi tersebut dibahas lain waktu. Kalau ada request untuk membuat materi mengenai identitas-isentitas Fibonacci, maka saya akan segera membuatnya.. ^^
Sekian, materi post ini. Semoga membantu menghilangkan penasaran kalian.. ^^